Złożoność obliczeniowa algorytmów to kluczowe zagadnienie do zrozumienia, w procesie tworzenia algorytmów. Bez jego znajomości, moim zdaniem, tworzenie efektywnych i szybkich algorytmów może być bardzo trudne, czy wręcz niemożliwe. W tym wpisie dowiesz się, czym jest złożoność obliczeniowa algorytmów, notacja dużego O, oraz poznasz najczęściej spotykane złożoności obliczeniowe.

Definicja algorytmu

Mówiąc o złożoności obliczeniowej algorytmów, warto na samym początku zdefiniować pojęcie algorytmu.

Często spotykanym opisem definiującym algorytm jest lista kroków w postaci przepisu na ciasto czy instrukcji wymiany koła w samochodzie. Takie przedstawienie algorytmu dla osoby nietechnicznej jest jak najbardziej akceptowalne. Pozwala to na zrozumienie tematu takiej osobie w stopniu dla niej akceptowalnym. Jednak takie przedstawienie definicji algorytmu w branży IT, moim zdaniem, jest niekompletne i wypada mizernie.

Algorytm to zestaw intrukcji, który dla zbioru danych x, należących do dopuszczalnego zbioru danych wejściowych, generuje rezultat y, należący do zbioru dopuszczalnych wyników, oraz spełnia następujące założenia:

1. Ma skończoną liczbę kroków. Niedopuszczalne jest stworzenie algorytmu nieskończonego.
2. Każdy krok algorytmu musi być obliczalny/wykonywalny.
3. Każdy krok algorytmu musi być zdefiniowany jednoznacznie. Przykładowo, niedopuszczalne jest zdefiniowanie kroku „wsyp cukier” – brakuje informacji: „gdzie?”, „ile?”.

Notacja dużego O

Notacja dużego O mówi nam o szybkości wykonania algorytmu. Przez szybkość mam na myśli tu ilość operacji, którą komputer musi wykonać, niekoniecznie zaś sam czas wykonania. Niemniej jednak spadek szybkości lubi iść w parze ze wzrostem czasu wykonania algorytmów.

Aby opisać algorytm za pomocą notacji dużego O, wykorzystuje się liczbę n, która wyraża liczbę elementów w zbiorze danych wejściowych przekazanych do algorytmu. Na podstawie liczby n każdy algorytm można opisać za pomocą formuły matematycznej mówiącej o liczbie operacji w kodzie, jaka musi się wykonać po podaniu zbioru wejściowego danych o rozmiarze n. Można również powiedzieć, że notacja dużego O opisuje, jak rośnie liczba operacji do wykonania przez algorytm wraz ze zwiększaniem się zbioru wejściowego.

Jednym z najprostszych przykładów złożoności obliczeniowej jest złożoność O(n). Taki poziom złożoności oznacza, że algorytm wykona tyle operacji, ile elementów będzie się znajdować w zbiorze danych wejściowych. Przykładem algorytmu o złożoności n jest poniższy prosty kod wykorzystujący pętlę for, która iteruje po zbiorze danych wejściowych.

const input: number[] = Array.from( Array( 100 ).keys() );

function multiplyBy2( input: number[] ) {
    const multipliedInput: number[] = [];

    for ( let i of input ) {
        multipliedInput.push( i*2 );
    }

    return multipliedInput;
}

console.log( multiplyBy2( input ) );

Bardzo istotnym aspektem opisywania złożoności obliczeniowej algorytmów z wykorzystaniem notacji dużego O jest fakt, że opisuje ona najmniej korzystny (najgorszy) przypadek z punktu widzenia wykonywanego algorytmu. Aby zobrazować to zagadnienie lepiej, zmodyfikowałem nieco powyższy kod.

const input1: number[] = Array.from( Array( 100 ).keys() );
const input2: number[] = Array.from( Array( 10 ).keys() );

function multiplyBy2( input: number[] ) {
    const multipliedInput: number[] = [];

    for ( let i of input ) {
        multipliedInput.push( i*2 );

         if( i*2 === 100 ) {
            return multipliedInput;
        }
    }

    return multipliedInput;
}

console.log( multiplyBy2( input1 ) );
console.log( multiplyBy2( input2 ) );

W przypadku zbioru danych input1 faktyczna liczba operacji w powyższym algorytmie nie wyniesie n, lecz ⁿ/₂. Nie zmienia to jednak złożoności obliczeniowej tego algorytmu, ponieważ można znaleźć zbiór „gorszy” z punktu widzenia ilości operacji do wykonania. Zbiorem „gorszym” w tym przypadku jest na przykład input2. Oznacza to również, że przykładowo, złożoność 7n² + 35n + 7 jest dalej złożonością n², pomimo faktu, że dla pustego zbioru danych liczba operacji wyniesie 7.

Dlaczego złożoność obliczeniowa jest istotna?

Algorytmy opisane za pomocą notacji dużego O warto rozważać w kontekście rosnących zbiorów danych. Dwa algorytmy wykonujące tę samą czynność, lecz mającą różną złożoność mogą drastycznie różnić się wydajnością i czasem wykonania. Przykładowo, mając zbiór danych o rozmiarze n = 10000, dwa algorytmy wykonujące tę samą czynność, gdzie jeden jest opisany O(n), a drugi O(n²) różnica w liczbie obliczeń wynosi:

• O(n) = 10000
• O(n²) = 100000000

Gdy przy pracy z algorytmem pojawia się skala, zmniejszenie złożoności potrafi przynieść ogromny wzrost wydajności.

Często spotykane złożoności obliczeniowe

W algorytmice pewne złożoności obliczeniowe występują znacznie częściej niż inne. W dalszej części wpsiu przedstawiam najczęściej spotykane złożoności obliczeniowe:

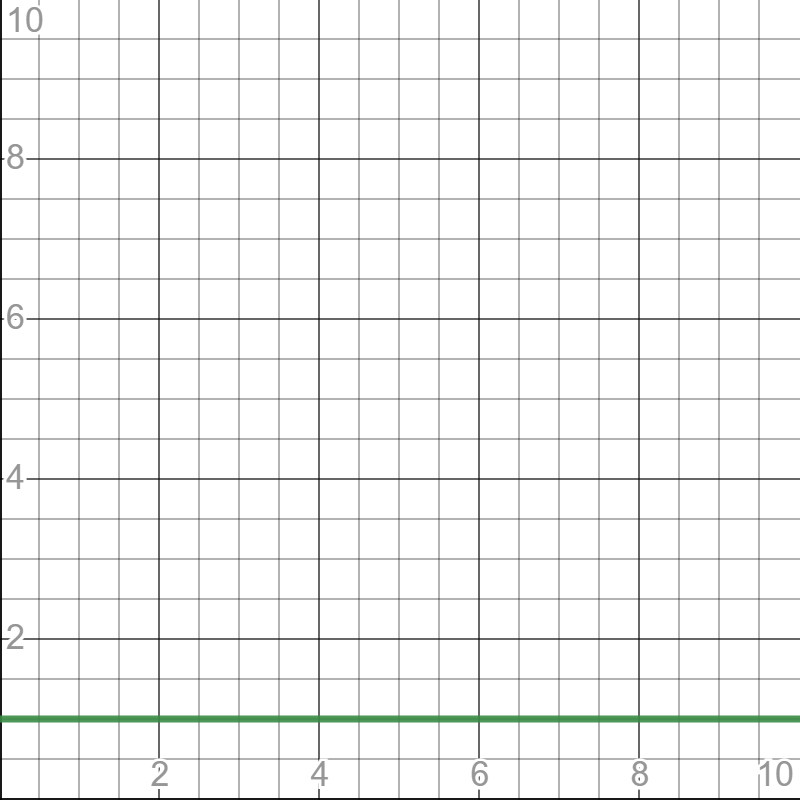
O(1)

Jest to stała złożoność obliczeniowa. Zamiast liczby 1 można umieścić dowolną inną liczbę. Taka złożoność oznacza, że liczba operacji w takim algorytmie zawsze będzie wynosić tyle, ile wynosi stała wartość, niezależnie od rozmiaru zbioru wejściowego.

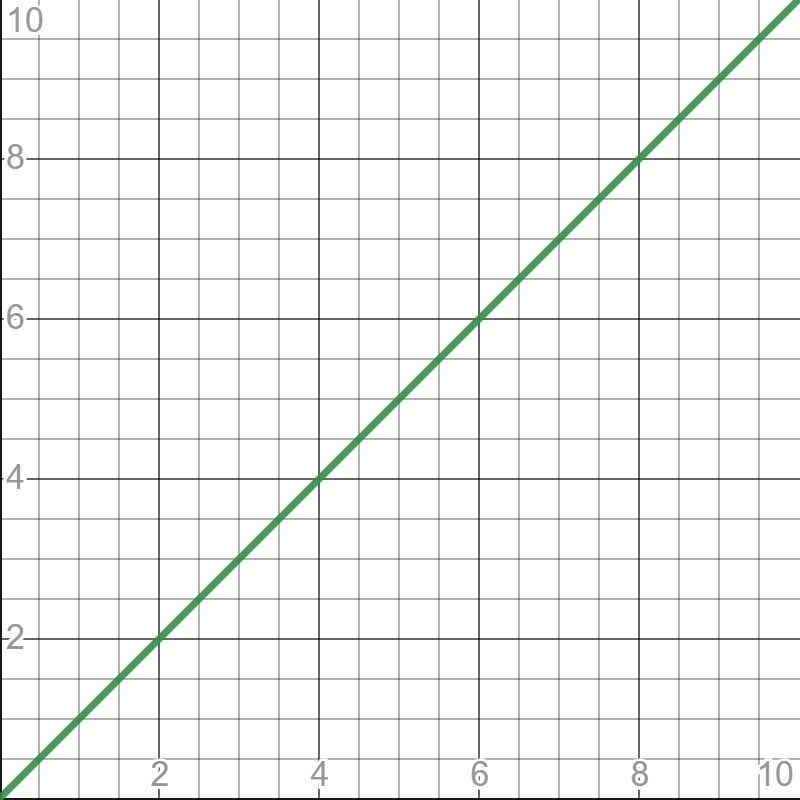
O(n)

Tę złożoność już de facto opisałem wcześniej. Liczba operacji w algorytmie rośnie liniowo w odniesieniu do rozmiaru zbioru wejściowego.

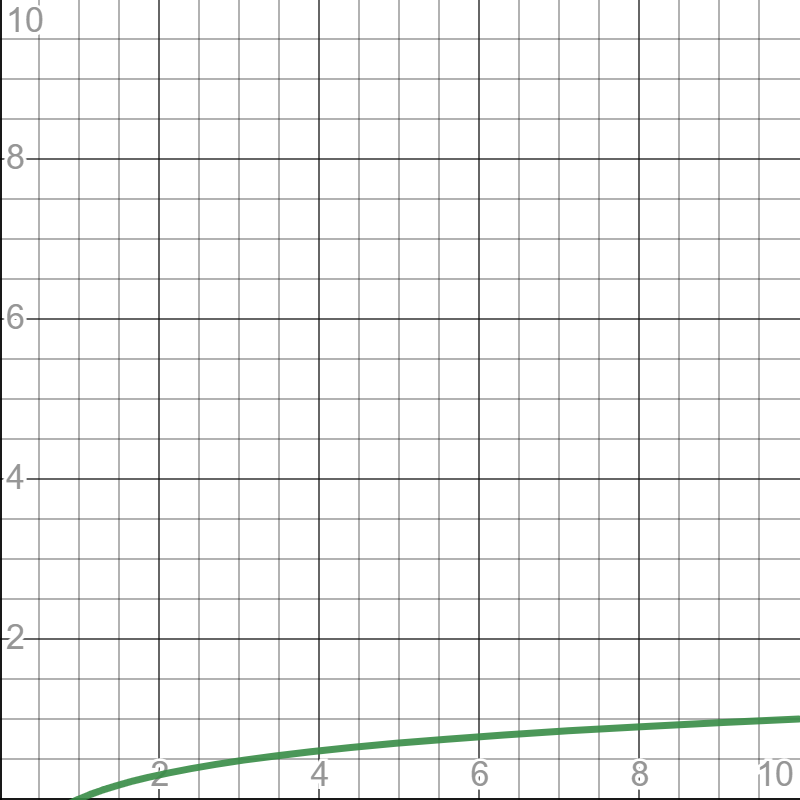
O(log n)

Jest to złożoność logarytmiczna. Oznacza to, że dla zbioru o rozmiarze 2ⁿ, liczba operacji wyniesie n. Tego typu złożoność często można spotkać w algorytmach wykorzystujących zasadę „dziel i rządź”, na przykład w algorytmie wyszukiwania binarnego.

O(n * log n)

Ten typ złożoności obliczeniowej często występuje w algorytmach sortowania, wykorzystujących zasadę „dziel i rządź”, na przykład w algorytmie sortowania przez łączenie (merge sort).

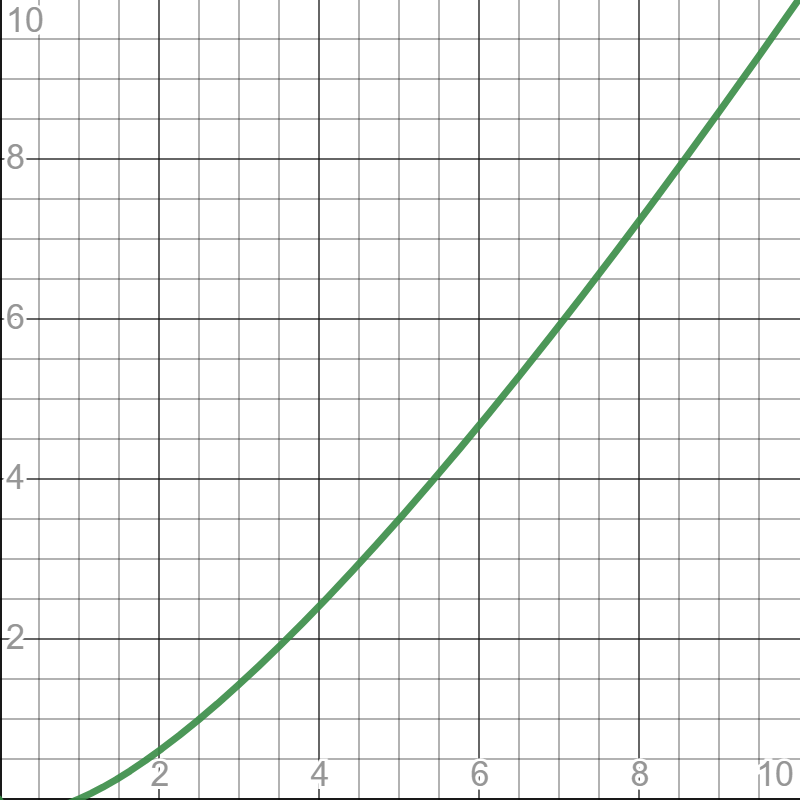
O(n²)

Tym wzorem opisana jest złożoność kwadratowa. Ten typ złożoności obliczeniowej występuje na przykład w algorytmach, które mają w sobie zagnieżdżoną pętlę for iterującą po całym zbiorze wejściowym. Stąd też, w miarę możliwości, warto rozważyć refaktoryzację kodu, jeśli w algorytmie występuje taka struktura.

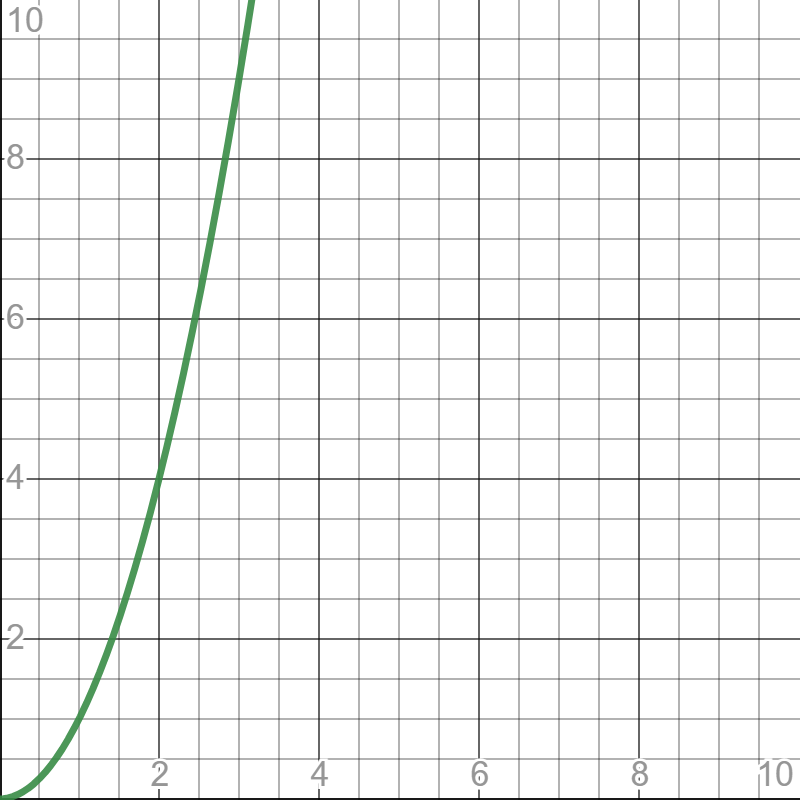
O(2ⁿ)

Jest to tzw. złożoność wykładnicza. W tym przypadku tak jak w przypadku stałej złożoności obliczeniowej liczbę 2 można zastąpić dowolną inną. Przykładem algorytmu wykorzystującego taką złożoność jest algorytm wykorzystywany przy ataku brutalnym (brute force attack). W przypadku hasła o długości n znaków, mającego jedynie małe litery wykorzystywane w języku angielskim oraz cyfry złożoność będzie wynosić O(36ⁿ).

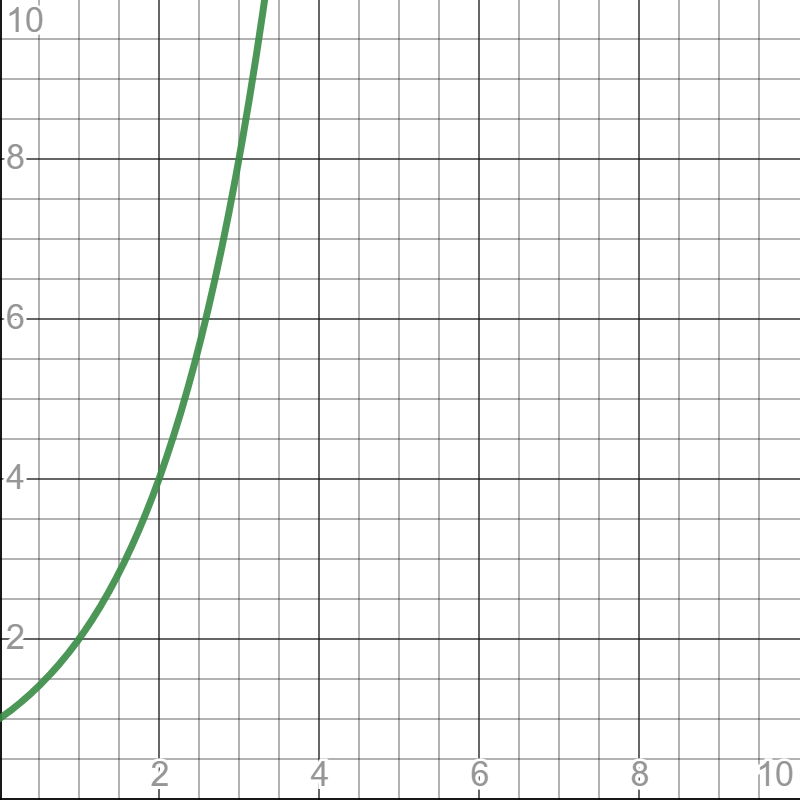
O(n!)

Złożoność obliczeniowa n! (n silnia) również „występuje w przyrodzie”. Przykładem algorytmu o złożoności obliczeniowej n! jest algorytm rozwiązujący problem komiwojażera.

Podsumowanie

Mam nadzieję, że dowiedziałeś/aś się czegoś nowego i że Twoje przyszłe algorytmy będą cechowały się jak najniższą złożonością. Serdecznie zachęcam do zapoznania się z materiałami dodatkowymi, źródłami, udostępnienia tego wpisu oraz zostawienia komentarza.

Źródła i materiały dodatkowe:

• Algorytmy – Ilustrowany przewodnik – Aditya Y. Bhargava
• Cracking the Coding Interview: 189 Programming Questions and Solutions – Gayle Laakmann McDowell
• What does O(log n) mean exactly?
• What’s the simple explanation for O(n log n)?
• Is Quick Sort a Divide & Conquer approach?
• Overview of quicksort
• Essential Programming | Time Complexity
• Big O notation
• #7. Złożoność obliczeniowa
• Podstawy złożoności obliczeniowej
• Złożoność obliczeniowa, czasowa i pamięciowa algorytmów

Zaobserwuj mnie na LinkedIn!

LinkedIn jest głównym medium, poza blogiem, gdzie publikuję swoje przemyślenia. Zaobserwuj mój profil na LinkedIn, by być na bieżąco!
Zachęcam też do zaobserwowania devszczepaniak.pl na Facebooku, gdzie oprócz informacji o nowych artykułach publikuję linki do ciekawych treści.

Udostępnij wpis

Szukasz taniego i dobrego VPS? Skorzystaj z Mikrusa i przy zakupie odbierz dodatkowy miesiąc usługi za darmo!

📖 Koniecznie sprawdź ofertę księgarni Helion oferującej tysiące książek dla programistów w dobrych cenach! Kupując z tego linku, pomagasz w rozwoju bloga.

Chcesz docenić moją pracę? Postaw mi kawę!